Example: Custom Contours Based on Weekly Headcount
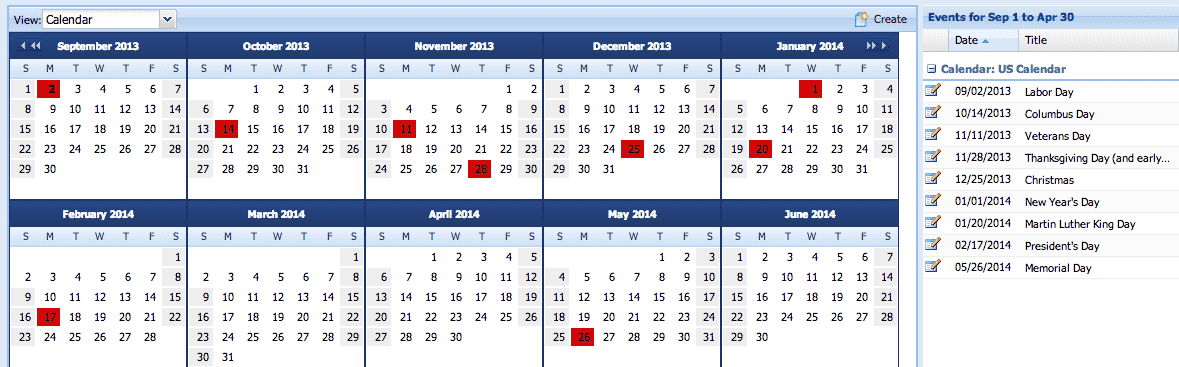
The following example uses this project calendar; working hours Monday through Friday from 9am to 5pm, with the following holidays:
Allocation Unit: Headcount
Contour Interval: Weekly
When you create an allocation in Headcount mode, initially the headcount value is placed uniformly across the date range. Allocations are in a custom headcount state if a user has made an edit to a contour, if, for example, a uniform headcount over the entire date range is not sufficient. The user might edit the value for a specific week (or weeks).
For example, create an allocation in Headcount mode, using weekly intervals. You'll start out with a contour of 1 in each interval (the Total Headcount value applied uniformly):

Now edit the headcount for the week starting 9/9/13 to "0.50":

You can view this allocation in Hours mode to see how PPM Pro calculates the hours.

-
Week 1 is defined by a Headcount of 1, meaning use all available working time for that week. Because Sept 9 is a holiday, there are 4 working days (8 hours/day) = 32 hours.
-
Week 2 is has a custom contour of 0.5, which means use half of the available working time for that week. This week has no holidays, so total working time is 5 days (8 hours/day) = 40. Half of that is 20.
-
52 / 72 = 0.72 headcount
Shifting
When you replan a custom contour, try to keep the units in Headcount mode as much as possible.
Shift by Weeks
Let's shift this contour by one week.

Notice that the Total Headcount in 0.75. Take a look at the allocation in Hours mode:

There are no holidays in the new date range, so the total available working time is 80 hours. In the previous date range, there were only 72 working hours.
-
Previous range (see baseline): 52 hours / 72 hours = 0.72
-
New date range: 60 hours / 80 hours = 0.75
The custom weekly contour [ 1.00, 0.50 ] was preserved and then reapplied over the new date range, resulting in a new calculation for Total Hours/Total Headcount.
Shift by Days
Let's shift by 3 days. The start date is still within the week 9/2/13, and the end date has moved into the next week. Note that the allocation now extends into a third week. PPM Pro copies the value from the second week to the third week.

You can look at this shift in terms of hours. Total hours is now only 40, while total available working time is 64 hours (8 working days with 8 hours/day). 40/64 = 0.625 (rounded to 0.63). This is the value you see as Total Headcount.

Another example: let's shift by 10 days:

Similar to the previous example, the custom contour is preserved and an additional interval is added to the allocation.
Shift by Months
Shifting by months works the same was as shifting by days.
Let's shift the original allocation by one month. This new date range covers 2 weekends, which removes two more working days from the equation. This is why the Headcount number is reduced.

If we shift another month out, the custom contour is still preserved - the last value (0.50) is repeated in the additional interval.

Extending
Extend by Weeks
Let's take the original contour and extend by one week. The custom contour is extended, and the last value of the contour is applied to the new week.

Extend by Days
Similar to extend by weeks, the custom contour is extended by applying the value of the last week into the future.
Extend by Months
Let's extend the allocation by one month. You can see that the value of the last week is copied into the new month.

If we view this allocation in monthly intervals, you can see that the individual contour values change:

It helps to view this monthly allocation in hours:

-
Sept 2 - Sept 13 has 72 hours of working time available. 52/72 = 0.72
-
Sept 2 - Sept 30 has 160 hours of working time. 96/160 = 0.6
-
Oct 1 - Oct 13 has 72 hours of working time. 36/72 = 0.5
You can see that extending a weekly custom contour by months, and then viewing it in months gives results that might not be obvious at first. When you convert to hours and do the math, you can see how the numbers are derived.

